इस लेख में हमारे द्वारा परवलय (Parabola) की परिभाषा , सूत्र तथा महत्वपूर्ण प्रश्नोतरी दिए गए है जो कक्षा 7 से 10 तथा 11 एवं 12 के लिए अतिमहत्वपूर्ण है | कक्षा 11 NCERT के लिए तो यह लेख बहुत ही फायदेमंद है | आप हमे नीचे comment करके बता सकते है कि आपको यह लेख कैसा लगा |
{tocify} $title={Table of Contents}Parabola ki paribhasha , sutra(Formula) aur Mahtvpurn Prashnotari :-
परवलय ( Parabola ) :-
अंग्रेजी भाषा में "Para" का अर्थ "से" तथा "bola" का अर्थ "फेंकना" होता है अर्थात् Parabola का अर्थ है - हवा में गेंद फेंकना से बना हुआ पथ
परवलय क्या है / परवलय की परिभाषा :-
यह एक द्विविमीय समतलीय वक्र होता है |
एक परवलय तल के उन सभी बिन्दुओं का समुच्चय है जो एक निश्चित सरल रेखा और तल के एक निश्चित बिंदु ( जो रेखा पर स्थित नही है ) से समान दूरी पर है यह अंग्रेजी अक्षर U
के आकार का होता है
परवलय की नियता :-
निश्चित सरल रेखा को परवलय की नियता ( directrix ) कहते है इसे l से व्यक्त किया जाता है
परवलय की नाभि :-
अक्ष पर स्थित निश्चित बिंदु F को परवलय की नाभि ( focus ) कहते है इसे F से व्यक्त किया जाता है
परवलय का अक्ष :-
परवलय की नाभि से जाने वाली तथा नियता पर लम्ब रेखा को परवलय का अक्ष कहते है
परवलय का शीर्ष :-
परवलय का अक्ष जिस बिंदु पर परवलय को काटता है उसे परवलय का शीर्ष ( Vertex ) कहते है इसे v से व्यक्त किया जाता है
नाभीय दूरी :-
परवलय की अक्ष पर नाभि तथा शीर्ष के बीच की दूरी , नाभीय दूरी कहलाती है |
परवलय की अपभ्रष्ट स्थिति :-
यदि निश्चित बिंदु , निश्चित सरल रेखा पर स्थित हो तो तल के उन बिन्दुओं का समुच्चय जो निश्चित बिंदु और निश्चित रेखा से समान दूरी पर है , निश्चित बिंदु से गुजरने वाली निश्चित रेखा पर लम्बवत सरल रेखा होती है | इस सरल रेखा को परवलय की " अपभ्रष्ट स्थिति " कहते है |
परवलय का व्यापक / प्रमाणित समीकरण सूत्र ( Standard equation of parabola ) :-
परवलय का समीकरण एक सरल समीकरण सूत्र है |
परवलय के चार संभव समीकरण निम्न प्रकार है -
(1) परवलय का प्रथम समीकरण सूत्र :-
जब परवलय x- अक्ष की धनात्मक दिशा के परित: सममित हो इसे दायी ओर खुला परवलय भी कहते है |
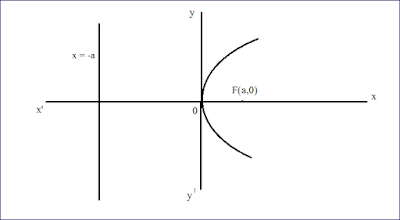
परवलय का समीकरण सूत्र y2 = 4ax
परवलय का शीर्ष = मूल बिंदु ( 0,0 )
परवलय की नाभि = F(a,0)
परवलय की नियता x = -a
परवलय का अक्ष = x- अक्ष की धनात्मक दिशा
परवलय की नाभि लम्ब जीवा की लम्बाई का सूत्र = 4a
परवलय का द्वितीय समीकरण सूत्र :-
जब परवलय x-अक्ष की ऋणात्मक दिशा के परित: सममित हो -
इसे बायीं ओर खुला परवलय भी कहते है
परवलय का समीकरण सूत्र y2 = -4ax
परवलय का शीर्ष = मूल बिंदु (0,0)
परवलय की नाभि = F(-a,0)
परवलय की नियता x= +a
परवलय का अक्ष = x- अक्ष की ऋणात्मक दिशा
परवलय का तृतीय समीकरण सूत्र :-
जब परवलय y-अक्ष की धनात्मक दिशा के परित सममित हो - इसे ऊपर की ओर खुला परवलय भी कहते है |
परवलय का समीकरण सूत्र x2 = 4ay
परवलय का शीर्ष = मूल बिंदु ( 0,0 )
परवलय की नाभि = F(0,a)
परवलय की नियता y = -a
परवलय का अक्ष = y- अक्ष की धनात्मक दिशा
परवलय का चतुर्थ समीकरण सूत्र :-
जब परवलय y-अक्ष की ऋणात्मक दिशा के परित: सममित हो | इसे नीचे की ओर खुला परवलय भी कहते है |
परवलय का समीकरण सूत्र x2 = -4ay
परवलय का शीर्ष = मूल बिंदु ( 0,0 )
परवलय की नाभि = F(0,-a)
परवलय की नियता y = +a
परवलय का अक्ष = y- अक्ष की ऋणात्मक दिशा
परवलय के इन्ही चारों समीकरणों को परवलय के मानक समीकरण सूत्र कहते है | उपरोक्त चारों समीकरण सूत्र परवलय के चार प्रकार कहलातें है |
परवलय की नाभिलम्ब जीवा :-
परवलय की नाभि से जाने वाली और परवलय की अक्ष के लम्बवत रेखाखण्ड जिसके अत्य बिंदु परवलय पर हों , को परवलय की नाभिलम्ब जीवा कहते है |
परवलय y2 = 4ax की नाभिलम्ब जीवा की लम्बाई का सूत्र -
नाभिलम्ब जीवा की लम्बाई का सूत्र = 4a
परवलय से सम्बंधित प्रश्नोतरी ( Parabola Questions and Answer ) :-
1. नाभि (2,0) और नियता x=-2 वाले परवलय का समीकरण ज्ञात करें ?
क्योकिं नाभि (2,0) x-अक्ष पर है इसलिए x-अक्ष पर है
इसलिए x-अक्ष स्वयं परवलय का अक्ष है
अत: परवलय का समीकरण -
y2 = 4ax या y2 = -4ax के रूप में होना चाहिए क्योकिं नियता x=-2 है और नाभि (2,0) है
इसलिए परवलय का समीकरण y2 = 4ax के रूप में है जहाँ a = 2
परवलय का अभीष्ट समीकरण -
y2 = 4ax
y2 = 4(2)x
y2 = 8x
2. एक परवलय का समीकरण ज्ञात कीजिए जिसका शीर्ष (0,0) और नाभि (0,2) है ?
यहाँ शीर्ष (0,0) पर और नाभि (0,2) पर है जो y-अक्ष पर स्थित है |
अत: परवलय का अक्ष y-अक्ष है
इसलिए परवलय का समीकरण x2 = 4ay के रूप में है
अत: परवलय का अभीष्ट समीकरण -
x2 = 4ay
x2 = 4(2)y
x2 = 8y
3. परवलय किसे कहते हैं ?
परवलय ऐसे बिन्दुओं का बिन्दुपथ है जिसका किसी निश्चित रेखा से दूरी , किसी निश्चित बिंदु से दूरी के बराबर होती है |
✹ इन्हें भी पढ़े :-
बेलन / खोखले बेलन के सूत्र
घन के सूत्र , गुण एवं नियम ( cube formula )
घनाभ के सूत्र , गुण एवं नियम ( cuboid formula )
चतुर्भुज के सूत्र ( chaturbhuj ke sutra )
त्रिभुज के प्रकार
त्रिभुज व त्रिभुज के महत्वपूर्ण गुण एवं नियम
चतुर्भुज के प्रकार ,उनके गुण एवं सूत्रों का अध्धयन
त्रिभुज के परिकेंद , अंत: केंद्र , गुरुत्व केंद्र एवं लंब केंद्र
Maths Notes की Free PDF यहां से Download करें
सभी बिषयवार Free PDF यहां से Download करें